第16問
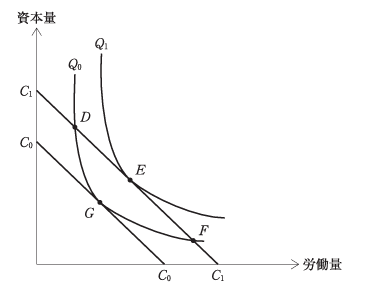
下図は、ある個人の予算制約線を描いている。当初の予算制約線はABであり、
このとき、この個人は点Eで決まる数量のX財とY財を消費している。所得の増
加によって予算制約線はCDとなり、このとき、この個人は点Fで決まる数量の
X財とY財を消費している。
この図に関する記述の正誤の組み合わせとして、最も適切なものを下記の解答群
から選べ
a X財の所得効果は、負である。
b X財の所得弾力性は、正である。
c Y財の所得効果は、負である。
d Y財の所得弾力性は、ゼロである。
- a:誤 b:正 c:誤 d:誤
- a:誤 b:正 c:正 d:誤
- a:誤 b:正 c:誤 d:正
- a:正 b:誤 c:誤 d:正
- a:正 b:誤 c:正 d:誤
正解!
不正解...
正解はa:誤 b:正 c:誤 d:正です。
問題に戻る
第17問
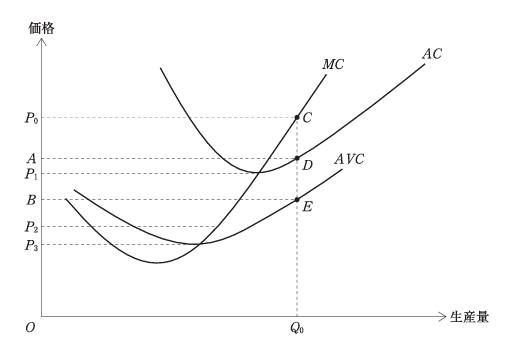
短期の完全競争市場下における価格と企業の生産との関係を考える。下図には、
ある財の生産に関する限界費用曲線MC、平均費用曲線ACおよび平均可変費用曲
線AVCが描かれており、価格が与えられると企業は最適生産を実現するものとす
る。ただし、P1はACの最小値、P3はAVCの最小値に対応している。
この図に基づいて、下記の設問に答えよ
(設問1)
価格がP0のときの生産者余剰として、最も適切なものはどれか。
- 四角形P0BEC
- 四角形AOQ0D
- 四角形BOQ0E
- 四角形ABED
- 四角形P0ADC
正解!
不正解...
正解は四角形P0BECです。
▶ 生産者余剰ってなに?
「モノを作って売るときに、“この価格で売れて助かった!”という企業の得した部分」です。
▶ どこまで作るの?
価格が P₀ のとき、企業は「価格 = 限界費用(MC)」となる点まで作るのがルール。
図では、それが生産量 Q₀、つまり 点C までです。
▶ 作るのにかかるお金は?
実際にモノを作るときにかかるお金は「可変費用」で、
それを表すのが AVC(平均可変費用)という曲線です。
生産量 Q₀ のときの AVC(=1個あたりの平均費用)は 点E に対応する価格(点Bの高さ)。
▶ 生産者余剰はどう出すの?
モノは Q₀ 個売る(横の長さ)
価格P₀(上の線)で売れた
かかった平均費用は AVC(点E・点Bの高さ)
だから、
(価格 − 平均費用)× 生産量 = (点Cと点Eの高さの差)× 点Cまでの横の長さ
→ 図形でいうと、四角形 P₀BEC
🧾 まとめ:この問題のポイント
観点 内容
生産量 限界費用MCと価格P₀が交わるところ → 点C=Q₀まで
可変費用 生産量Q₀のときのAVC → 点E(高さは点B)
生産者余剰の面積 価格とAVCの差 × 数量 → 図形としては「P₀BEC」
正解 オ:四角形P₀BEC
問題に戻る
第18問
この図に関する記述の正誤の組み合わせとして、最も適切なものを下記の解答
群から選べ。
a 価格がP1のとき、企業の総収入は可変費用と固定費用の合計に等しくなる。
b 価格がP2のとき、企業の損失は固定費用の一部のみとなる。
c 価格がP3のとき、企業の損失は可変費用のみとなる。
- a:正 b:正 c:誤
- a:誤 b:誤 c:誤 d:正
- a:正 b:正 c:正
- a:誤 b:正 c:正
- a:正 b:誤 c:誤
正解!
不正解...
正解はa:正 b:正 c:誤です。
a.価格が P₁ のとき、企業の総収入は可変費用と固定費用の合計に等しくなる。
P₁ は AC(平均費用) の最小値。
AC×Q₀=総費用、P₁×Q₀=総収入。
つまり「収入=費用」の時点 ⇒ 損益分岐点。
可変費用+固定費用=総費用なので、等しくなる。
→ ✅ 正しい
b.価格が P₂ のとき、企業の損失は固定費用の一部のみとなる。
P₂ は AVC(平均可変費用) より上、ACより下。
よって収入は可変費用より多いが、総費用より少ない
つまり、「可変費用はカバーしているが、固定費用の一部だけ回収できない」状態。
→ ✅ 正しい
c.価格が P₃ のとき、企業の損失は可変費用のみとなる。
P₃ は AVCの最小値(=限界点)であり、損失=固定費用すべて。
可変費用はちょうど回収できるが、固定費用はすべて損失になる。
よって、「可変費用のみが損失」ではない。
→ ❌ 誤り
b.消費者余剰は、三角形ABFである。
✅ 結論:正しい
✅ 解説:
この図は、1社がすべてを販売している独占市場を前提としています。
独占企業は、「限界収入(MR)=限界費用(MC)」となる点(図の点H)まで生産し、
そのときの生産量に対応する価格(需要曲線上)=点F(価格B)で商品を売ります。
💡 独占市場における特徴
価格は「需要曲線における値」 → 点F(価格B)
生産量は、完全競争に比べて少ない(点Iではなく点Hまで)
結果として、消費者にとっては
数量が少ない
価格が高い
よって、消費者余剰は小さくなります
📌 消費者余剰の意味と図形:
消費者余剰=「支払ってもよい価格」と「実際の支払い価格」の差の合計
この図での消費者余剰は:
上限:需要曲線(AD)
実際の価格:点F(価格B)
購入数量:点Hまで
よって、三角形ABF が、独占下における消費者余剰を表します。
c.生産者余剰は、四角形CEHGである。
✅ 結論:誤り
🔍 図の構造から確認:
独占企業は、MR=MCとなる点Hまで生産する。
売れる価格は、点F(価格B)で、点Hに対応する需要曲線上の点
よって、
販売価格(上辺):B(点Fの高さ)
限界費用(下辺):MC曲線の点H(価格は明記されていないがCとしましょう)
生産量:OH(点Hまでの横の長さ)
📌 生産者余剰とは?
生産者余剰=販売価格と限界費用の差によって「企業が得する部分」
つまり、価格BとMC曲線との間の面積(0〜H)
❌ なぜ「四角形CEHG」は間違いなのか?
CEHGという図形には、
左辺C(価格)からEまで下に延びる線が含まれるが、これは使わない
点CがMC曲線の右側であり、実際の販売価格Bを表していない
正しい図形は:
四角形BFHG(価格BとMCの差 × 数量OH)
d.このとき生じる死荷重は、三角形FGIである。
社会的に望ましい生産量は需要曲線DとMCの交点=点I
独占では、点Hまでしか作らない(点Iより少ない)
死荷重は「本来なら得られたはずの社会的利益」
それを表すのは三角形FHI(価格BからMCとの交点Iまで)
→ ❌ d:誤(図の面積FGIではなく、正確には三角形FHI)
問題に戻る
第19問
下図は、ある財の生産販売を1社が完全に独占した市場を示している。この財の
需要曲線がDであり、MCが生産者の限界費用、MRが同じく限界収入である。こ
こで、独占企業は利潤を最大化するように、価格と生産量を決定するものとする。
この図に基づき、独占均衡に関する記述の正誤の組み合わせとして、最も適切な
ものを下記の解答群から選べ。
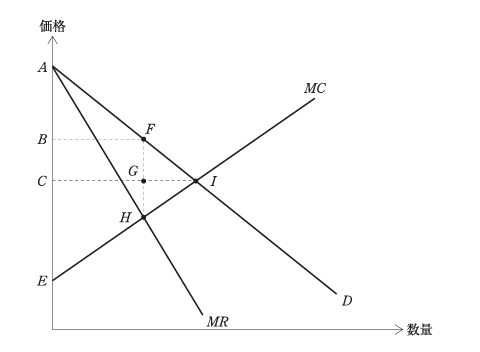
a 企業は価格をCとすることで利潤を最大化できる。
b 消費者余剰は、三角形ABFである。
c 生産者余剰は、四角形CEHGである。
d このとき生じる死荷重は、三角形FGIである。
- a:正 b:誤 c:正 d:誤
- a:正 b:誤 c:正 d:正
- a:誤 b:正 c:正 d:正
- a:誤 b:正 c:誤 d:誤
- a:正 b:正 c:誤 d:正
正解!
不正解...
正解はa:誤 b:正 c:誤 d:誤です。
a.企業は価格をCとすることで利潤を最大化できる。
点HでMR=MC → ここが独占企業の最適生産量
この生産量に対応する価格は、需要曲線D上の点Fの価格=B
よって企業は価格B(点F)で販売する
したがって「価格Cでは利潤最大化できる」という記述は誤り
→ ❌ a:誤
問題に戻る
第20問
下図は、ある観光資源に関する消費の外部不経済を示している。観光客の増加に
伴う交通渋滞やゴミの投棄など、観光資源の消費は近隣の環境や住民に無視できな
い損害を生じさせる場合がある。観光資源に対する消費者(観光客)の限界価値曲線
はD0であるが、第三者への損害を考慮した場合の社会的限界価値曲線はD1である。
この図に関する記述として、最も適切な組み合わせを下記の解答群から選べ。

a 完全競争市場での均衡下で生じる死荷重は、四角形GFHEである。
b 完全競争市場での均衡下での外部不経済は、四角形CAHEである。
c 社会的に最適な消費が実現したときの社会的余剰は、四角形CBFGである。
d 社会的に最適な消費が実現したときの外部不経済は、四角形CAFGである。
- aとd
- aとb
- bとd
- bとc
正解!
不正解...
正解はbとdです。
✅ 問題の背景(前提)
この図は、観光資源の利用による 消費の外部不経済 を示しています。
観光客が増えると、交通渋滞やごみなど**第三者に損害(外部不経済)**を与える。
観光客自身の限界価値(需要曲線):D₀
外部不経済を含めた社会全体の限界価値:D₁(D₀より低くなる)
供給曲線(限界費用):S
✅ 各点の定義
F:D₁とSの交点 → 社会的に望ましい最適消費量(外部不経済を考慮)
E:D₀とSの交点 → 実際の市場での消費量(外部不経済は無視)
A:数量ゼロのときのD₁上の価格(縦軸切片)
B:数量ゼロのときのS上の価格(縦軸切片)
G:Fの数量に対応するD₀上の点(需要曲線D₀上の価格)
H:Eの数量に対応するD₁上の点(社会的限界価値)
✅ 各選択肢の正誤と解説
a:完全競争市場での均衡下で生じる死荷重は、四角形GFHEである。
❌ 誤り
死荷重とは、「本来得られたはずの社会的余剰が失われた部分」。
最適消費量Fを超えて、Eまで消費されてしまったことで発生。
この部分の D₁とSの差 に相当する三角形 GFH が死荷重。
四角形GFHEとすると、D₀との価格差も含んでしまうため誤り。
b:完全競争市場での均衡下での外部不経済は、四角形CAHEである。
✅ 正しい
外部不経済とは、「消費者が評価している価値(D₀)」と「社会的な価値(D₁)」の差。
数量0〜Eまでにわたる、D₀とD₁の差を表す面積が外部不経済。
これは、図形でいうと四角形 CAHE に相当する。
c:社会的に最適な消費が実現したときの社会的余剰は、四角形CBFGである。
❌ 誤り
最適な消費量は F。
社会的余剰は、数量0〜Fまでの間で「D₁とSの差」でできる面積。
正しい図形は 三角形ABF。
四角形CBFGはD₀や他の関係を含む誤り。
d:社会的に最適な消費が実現したときの外部不経済は、四角形CAFGである。
✅ 正しい
社会的に最適な消費に止めた場合(F)、Eまで消費されないため外部不経済は軽減。
しかし、最初から存在していた外部不経済(0〜FのD₀とD₁の差)は残る。
この面積は 四角形CAFG。
✅ 正解:エ(bとd)
問題に戻る



この問題は、「所得の変化によって消費量がどう変わったか(=所得効果)」をもとに、各財の**性質(上級財・劣等財)**を判断するものです。
図の読み取り
所得増加により予算線が AB → CD に平行移動(価格比は一定)
点E → 点F への移動により:
X財の消費量は増加
Y財の消費量は変化なし
🧠 各選択肢の正誤判断
a:X財の所得効果は、負である。
誤り(×)
👉 所得が増えたらX財の消費量は増加している → 所得効果は正(上級財)
b:X財の所得弾力性は、正である。
正しい(〇)
👉 所得↑ → 消費量↑ → 所得弾力性は正の値
c:Y財の所得効果は、負である。
誤り(×)
👉 所得が増えてもY財の消費量は変わっていない → 所得効果はゼロ
d:Y財の所得弾力性は、ゼロである。
正しい(〇)
👉 所得が変化してもY財の消費量は不変 → 所得弾力性はゼロ
✅ 正解は
a:誤 b:正 c:誤 d:正